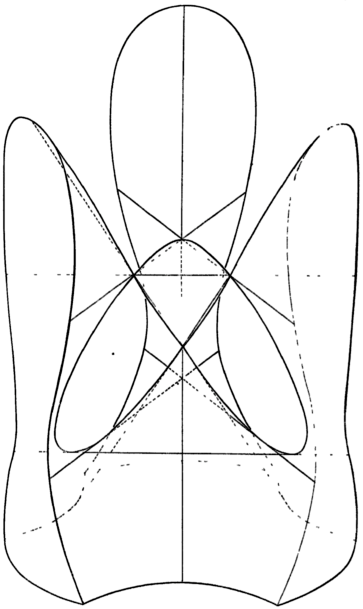
C’est l’objet mathématique que l’on aperçoit dans une vitrine de l’Exposition surréaliste d’objets de 1936 à la galerie Charles Ratton: voir Werner (2002), page 149, qui suppose à tort que c’est un exemplaire du modèle 44 (VII, 1).
Ce modèle exhibe une courbe asymptote, tracée en jaune, ainsi que les droites de cette surface cubique.
Cette surface a été réalisée une deuxième fois dans la série des surfaces cubiques par Carl Rodenberg: c’est le modèle 45 (VII, 2). Dans cette deuxième réalisation, on met l’accent sur les 27 droites de la surface. Elles se répartissent ainsi: chacune des 6 droites reliant deux points doubles, tracées à l’origine en rouge, est de multiplicité 4; il en reste 3, qui sont laissées blanches.
45. (VII, 2.) Fläche mit 4 reellen conischen Knotenpunkten *). Man erhält dieselbe aus der Diagonalfläche durch Zusammenziehen der 4 Hälse. Von den 27 Geraden sind in die 6 Kanten des aus den Knoten gebildeten Tetraeders zusammengerückt.
Beseitigt man einen Teil der Knoten durch Abschnüren, während man die anderen wieder in Hälse verwandelt, so erhält man einen der Flächentypen mit weniger als 27 Geraden. Beim Abschnüren z. B. eines Knotens werden Gerade imaginär, man hat also den Typus einer Fläche mit nur 15 reellen Geraden u. s. f.
In die 6 roten Verbindungsstrahlen je zweier Knoten (Knotenstrahlen) sind je 4 Gerade hinein gefallen; die 3 weissen Geraden dagegen sind einfach (unär). Der durch die 4 Eckpunkte bestimmte tetraederförmige Flächenteil liegt ganz im Endlichen und ist positiv gekrümmt. (13×15 cm.) Mk. 12.—.
*) Die Buchstaben , , bedeuten conische, biplanare, uniplanare Knoten; der angehängte Zeiger gibt die Anzahl der Einheiten an, um welche die Klasse durch die betreffende Singularität erniedrigt wird.
Voici les références de ce deuxième modèle: Schilling, série VII (1881) no 2 pages 14-16 et 45 pages 116-117. Dyck, 163 Specialkatalog 31 pages 263-264. Fischer (1986b), pages 12-14, photographie 13. Vierling-Claassen (2007), modèle 20, pages 55-56. Il est présent à
Göttingen,
Groningue,
Halle,
Harvard,
Italie,
Pavie,
Pavie.

212. (II, 2.) Fläche 3. Ord. vierter Classe mit 4 reellen conischen Knoten, auf welche eine Asymptotencurve (gelb) aufgezeichnet ist; sie entspricht dualistisch einer Asymptotencurve der Steiner’schen Fläche (4. Ord., dritter Classe) und ist nach Clebsch (Crelle Bd. 67, S. 9) eine Raumcurve 6. Ord., vierter Classe, die in jedem Knotenpunkt der Fläche einen Rückkehrpunkt besitzt. Von Bacharach in München (B). Erläuterung beigegeben. (13×22 cm.) Mk. 16.50.
Schilling, série II (1877) no 2 pages 5-6 et 212 page 141. Dyck, 211 Specialkatalog 125 page 289. Maillard et Belgodère, 134. Campedelli, gruppo C N. 2.
Göttingen, Marbourg, Vienne. Moulages réalisés sous la direction de Luigi Campedelli en 1952: Milan, Turin.